Comment citer ce document ?
Jacques-Deric Rouault, 2012. Escher et Moebius. Rastell Toull page C114.
Dans le bandeau des articles relatif à la recherche scientifique,
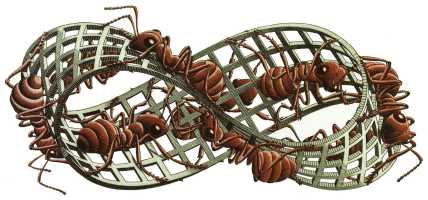
l'image située à gauche représente des fourmis marchant sur un anneau de Möebius, d'après une
gravure de Ernst Escher.
Augustus Ferdinand Möbius (ou Moebius) est un
mathématicien et astronome allemand qui vécut de 1790 à 1868. Il est
connu comme l'inventeur en 1868 de l'anneau de Möbius, la fonction de
Möbius, le slip de Möbius, et les tétraèdres de Möbius.
L'anneau (ruban, bande, ceinture, surface, ...) de
Möbius a été découvert indépendamment par Johann Benedict Listing la
même (1858), qui en a décrit les propriétés topologiques. On devrait
donc parler de l'anneau de Möbius-Listing ou de Listing-Möbius.
Un anneau de Möbius qui illustre
la rubrique correspondante de Wikipedia
Il s'agit d'une surface obtenue en collant bord
à bord les petits cotés d'un rectangle long après avoir effectué une
torsion de la bande. Cette surface à deux dimensions plongée dans un
espace à trois dimensions possède des propriétés étonnante, car elle
n'a qu'un coté et qu'un bord.
La création de cette curiosité mathématique est
totalement évidente a posteriori. Je me pose aujopurd'hui la question
de savoir pourquoi elle n'a été découverte qu'en 1858, et pas avant, en
particulier par les mathématiciens grecs, si férus de paradoxes
... Et pourtant, à cette époque, on connaissait depuis longtemps
les ceintures de cuir, les rubans et les frises géométriques ... Je ne
vois aucune explication, à part une nouvelle version de l'oeuf de
Colomb : Il suffisait d'y penser !
mais cela n'explique rien ...
Escher et l'anneau de Möbius
|
Maurits Cornelis Escher est un graveur
néerlandais du XXe siècle (1898-1972). Il n'a produit qu'une centaine
de gravures sur bois, mais elles sont mondialement connues. Il a
produit plusieurs rubans de Möbius
Les oiseaux (ou cygnes) de Moebius
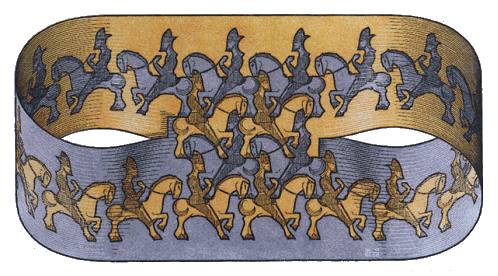Les cavaliers de Moebius
Un ruban de Möbius, sénestre à
trois demis-tours, découpé en son milieu, qui donne un noeud en trefle
Mais le plus extraordinaire est surement cet anneau de Möbius que
parcourent sans fin neuf fourmis, avec un rendu extraordinaire
Cliquer sur l'image pour
l'agrandir
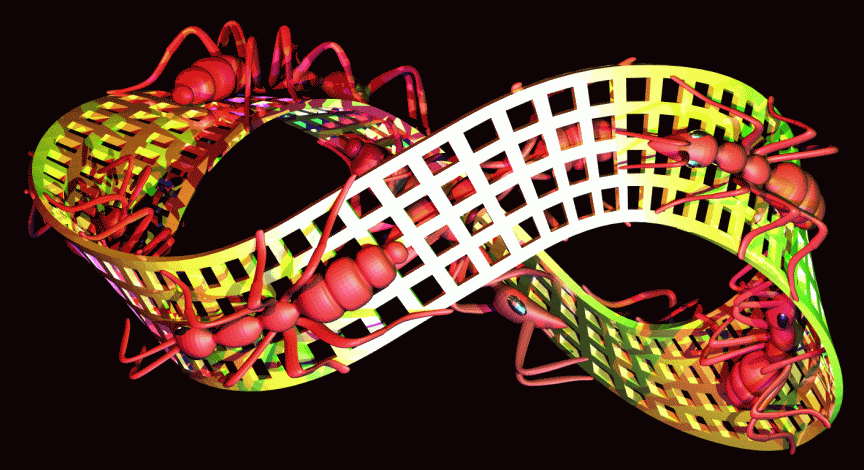
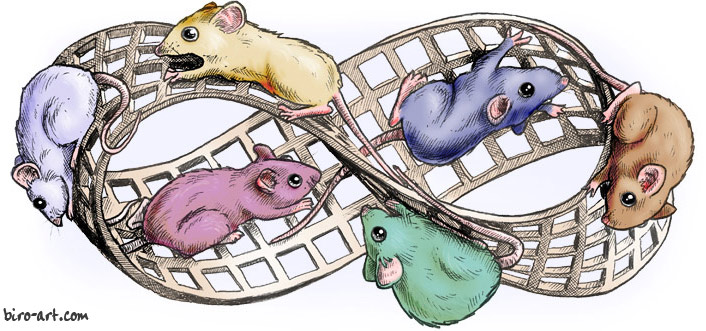
Cette image a beaucoup inspiré des artistes contemporains. Voici des
variations :
Pour l'image qui figure sur le
bandeau, nous avons sélectionné une image animée (format GIF). Dans
son oeuvre, Moebius a traité à plusieurs reprises l'anneau de Moebius.
J'ai été particulièrement séduit par la gravure qui représente 9
fourmis qui parcourent le ruban, parce qu'elle réunit à la fois la
Mathématique (l'anneau de Möbius est une topologie mathématique très
intéressante), l'Entomologie (science des insectes : il y a 9
fourmis en mouvement), et la Métaphysique (une des disciplines de la
philosophie : quel peut bien être le sens de la vie pour ces 9 fourmis,
sinon celui du mythe de Sysiphe ? Mais faut-il aller jusqu'à imaginer
ces fourmis heureuses ?). La réunion de ces trois disciplines résume
parfaitement mes aspirations et ma formation, car après une maitrise de
mathématique, j'ai
directement enchainé sur un DEA d'entomologie ... sans oublier un bac
Philo qui a succédé à un bac Math-Elem ... Oui, il faut oser ... Alors
j'assume pleinement,
je suis de ceux qui osent oser ! ... Et comme, avec l'âge, les
choses ne s'arrangent pas, j'ose aujourd'hui ce site web dévolu à une
nouvelle revue scientifique !!!
De
plus, cette gravure d'Escher
contient une magnifique question épistémologique : comment ces 9
fourmis se représentent-elles l'espace dans lequel elles vivent ? C'est
un monde étroit en largeur et qui parait infini en longueur. En fait,
si une fourmi marque par une substance chimique un endroit particulier
de son parcours, comme le
font toutes les fourmis du monde, elle retrouvera sa marque un peu plus
tard : elle vit donc dans un monde fini et circulaire, de la forme d'un
ruban.
Et en marquant asymétriquement son parcours, notre fourmi pourra
démontrer mathématiquement que son univers n'a qu'une seule face
et un seul bord. Maintenant, si une
fourmi volante arrive d'un autre monde et leur annonce qu'elles se
trompent complètement
car l'espace réel dans lequel elles vivent est euclidien, a trois
dimensions et est infini,
l'étrangère va, dans le meilleur des cas,
se faire traiter d'hétérodoxe, et il est plus que probable que les 9
fourmis orthodoxes d'Escher vont se jeter sur elle et s'empresser de
lui couper
ses ailes pour lui démontrer que c'est bien elles qui ont raison ...
Ainsi va le monde ...
On trouve sur le web une
autre image
animée.
Je
ne sais pas qui est l'auteur de cette image animée, directement
inspirée
de l'oeuvre d'Escher, que j'ai choisie comme identificateur visuel.
Elle se retrouve sur plusieurs sites, sans que la source en soit
référencée, ce qui indique que ce document est de facto tombé dans le
domaine public. Je remercie très chaleureusement le créateur inconnu de
cette
animation.
L'anneau de Möbius
Bouvier A, George M, Le Lionnais F, 1979-1983. Dictionnaire des
mathématisues. Presses Universitaires de France. 833 pp.
http://fr.wikipedia.org/wiki/August_Ferdinand_M%C3%B6bius
http://fr.wikipedia.org/wiki/Johann_Benedict_Listing
http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius
http://fr.wikipedia.org/wiki/%C5%92uf_de_Colomb
http://www.mathcurve.com/surfaces/mobius/mobius.shtml
Escher
http://fr.wikipedia.org/wiki/Maurits_Cornelis_Escher
http://www.mathcurve.com/surfaces/mobius/mobius.shtml
http://www.cs.technion.ac.il/~gershon/EscherForReal/
http://www.biro-art.com/mousemobius.html
http://forum.rollingstone.de/showthread.php?t=35030&page=48
http://ymonka.free.fr/maths-et-tiques/index.php/detentes/tableaux-et-gravures-celebres
http://www.allposters.fr/-st/Le-ruban-de-Moebius-II-Escher-Affiches_c95837_.htm
http://britton.disted.camosun.bc.ca/escher/moebius_strip_II.jpg
Images animées
http://eljjdx.canalblog.com/archives/2006/12/26/3511030.html
http://www.mathcurve.com/surfaces/mobius/mobius.shtml
http://www.moillusions.com/2006/10/eschers-moebius-ring-with-ants.html
Le mythe de Sysiphe
http://fr.wikipedia.org/wiki/Sisyphe
http://fr.wikipedia.org/wiki/Le_Mythe_de_Sisyphe
Autolien
Cette page utilise les articles
Articles utilisant cette page
Articles connexes
