Rastell Toull Site web consacrée à la Bretagne, à l'Afrique du nord à la chanson française, à la recherche scientifique, et à bien d'autres sujets ...

The monoalpha-multinumeric numeral system  : a numeration compatible with the lexicographic order and concatenation par Jacques-Deric Rouault Article original

Page publique Page opérationnelle Version 4.1 du 4 mai 2012 Table thématique Table chronologique Administrateur du site

This monoalpha-multidecimal numeration is written as follows : A0, A1, A2, ..., A9, B10, B11, ..., B99, C100, C101, ..., C999, D1000, D1001, etc ...

The compatibility with the alphanumeric sort is complete (property false for the decimal numeration) and the compactness is optimal because only a single figure is added to the classical decimal writing.

The greatest expressible value in this numeration is 10²⁶-1, usually convenient for all common applications.

Coding numbers by letters was relatively common in the antiquity, in particular in the Hebraic and Greek civilizations (Ifrah, 1981). However in these alphabets, if the 9 first letters code the units, the 10 following ones codes tens and the last letters the first hundreds. It however exists an archaic system of numeration based on the 24 Greek letters, dated form the VI century BC, and analogous to the one desrcibed here. This system, which does not exceed 24, was in particular used to number the 24 books of Iliad and Odyssey (Reinach, 1885).

The kind of code we propose here can also be compared to the code of variable length strings in some computer languages. In the string of characters, each character is coded by one byte (value in 0..255), and there is an extra first byte coding the actual number of bytes present in the string. In other languages, the string is completed by a byte with a predefined value (usually ASCII 3) which marks the end of the string, in the same manner as a stop codon in a DNA sequence.

The complete structuration of the monoalpha-multidecimal numeration can also be interpreted as integrating a redundancy check, as even bits (Spataru 1987). thus warranting the integrity when transferring or storing data. All possible sequences are not valid, for instance the numbers 1B2 and B123 are obviously wrong and show a corruptness of data.

In order to increase the readability of large integer numbers, a separator symbol (blank, point in French language, comma in English language) is usually added every 3 decimals. This use remains compatible with the monoalpha-multidecimal numeration, under the constraint it is applied to all numbers of the serial. Because of reasons of compatibility with the different operating systems of computers, the choice of the underscore character (ASCII 95) used for writing numbers in the ADA language (Taft & Duff, 1997) is highly recommended.

This method of prefixing with a Latin figure can also be extended to binary, hexadecimal, …, numerations.

    The direct concatenation of two or several integers can be read as a single integer or as several integers written in a fixed format. For instance le number 20080611 can also be considered as the eleventh day of the sixth month of 2008 in the fixed format YYYYMMDD. In order to remove any ambiguity, the writing D2008A6B11 clearly shows that this number is a concatenation of three integers. Because in the ASCII table integers (codes 48-57) are ranked before upper-case letters (65-90) and lower-case letters (97-122), the concatenation of monoalpha-multidecimal numbers is wholly compatible with the lexicographic order. A1B12 is before B12A1 because A is before B, A1C124 is before A1D1308 because C is before D.

    In a tree, the name of a branch is the concatenation or the name of the previous branch and of the rank of the branch at the node. The use of the monoalpha-multidecimal numeration provides a natural way to name all the branches in an order compatible with the lexicographic order (Figure 1)

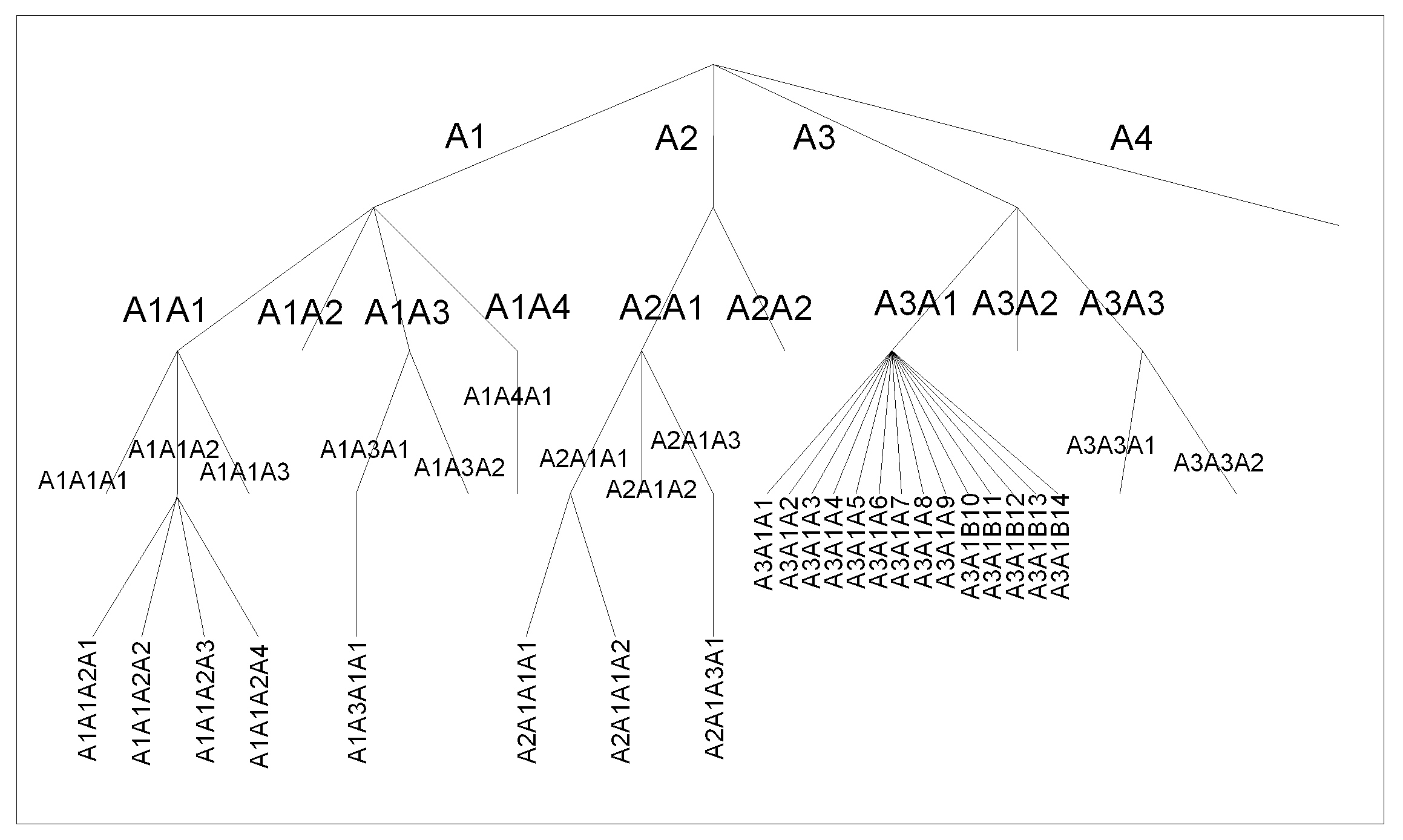
Figure 1 : Naming the branches of a tree by concatening monoalpha-multidecimal numbers

 
    In the tree of figure 1, the names of the 46 branches are automatically ranked in the lexicographic order A1, A1A1, A1A1A1, A1A1A2, A1A1A2A1, A1A1A2A2, A1A1A2A3, A1A1A2A4, A1A1A3, A1A2, A1A3, A1A3A1, A1A3A1A1, A1A3A2, A1A4, A1A4A1, A2, A2A1, A2A1A1, A2A1A1A1, A2A1A1A2, A2A1A2, A2A1A3, A2A1A3A1, A2A2, A3, A3A1, A3A1A1, A3A1A2, A3A1A3, A3A1A4, A3A1A5, A3A1A6, A3A1A7, A3A1A8, A3A1A9, A3A1B10, A3A1B11, A3A1B12, A3A1B13, A3A1B14, A3A2, A3A3, A3A3A1, A3A3A2, A4. The lexicographic order describes the tree by taking first at each node the rightest branch. Even for a branch at the fourth level, the name (for instance A2A1A3A1) remains easily readable.

    The monoalpha-multidecimal numeration was previously developed in the particular context of building up a data base devoted to an exhaustive census of transposable elements. They are short DNA sequences more or less highly repeated in the genomes of living organisms. A same transposable element can be found in different organisms, and will therefore be identified under different names in the available data banks. From the fact that two transposable elements presenting different lengths will be necessarily different, the transposable elements are then coded following their number of pairs of bases using the monoalpha-multidecimal numeration. The name of a sequence is built as the concatenation of the two numbers coding their length and their order of appearance, for instance C451B48. Comparing a new element to those previously recorded is then strongly accelerated following a process of quick sort, because one need only to compare it with those of the same length, which names becomes with the same first number.