
Site web consacrée à la Bretagne,
à l'Afrique du nord
à la chanson française,
à la recherche scientifique,
et à bien d'autres sujets ...
par Jacques-Deric Rouault
Article original
Page opérationnelle
Version 4.1 du
4 Mai 2012
Table thématique
Table chronologique
Administrateur du site
 (probabilité de réaliser A et B en deux tirages indépendamment de
l'ordre) par P(B) (probabilité de réaliser B) :
(probabilité de réaliser A et B en deux tirages indépendamment de
l'ordre) par P(B) (probabilité de réaliser B) :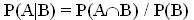 (1)
(1) 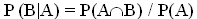 (2)
(2) 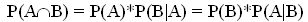 (3)
(3) 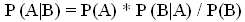 (4)
(4) (5)
(5)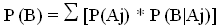 (6)
(6)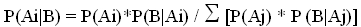 (7)
(7)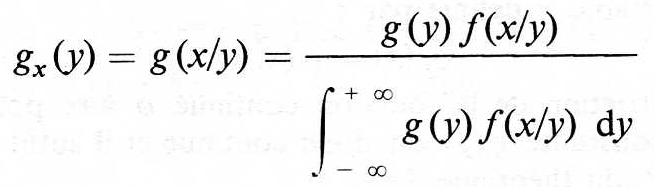
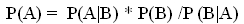 (9)
(9)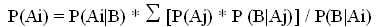 (10)
(10)